Data Structures

Teo, 26 June 2020

What are data structures?

Data structure are specialized formats for organizing, processing, retrieving and storing data. While there are several basic and advanced structure types, any data structure is efficient in some operations and inefficient in others. Therefore, the goal is to understand them in order to pick the most optimal data structure for the problem at hand.

Commonly used Data Structures are the following (listed from the easiest to wrap your head around to the hardest in my opinion):

Arrays
Linked Lists
Stacks
Queues
Trees
Graphs
Hash Tables

Arrays

An array is the simplest and most widely used data structure. Other data structures like stacks and queues are derived from arrays. Here’s an image of a simple array of size 10, containing elements [10, 20, 30, 40, 50, 60, 70, 80, 90 and 100].

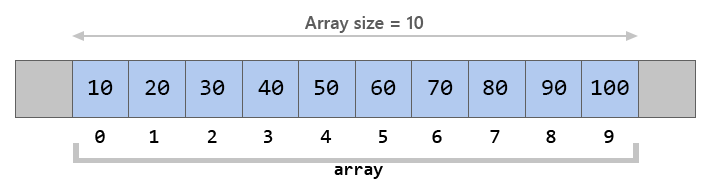Each data element is assigned a positive numerical value called the Index, which corresponds to the position of that item in the array. The majority of languages define the starting index of the array as 0.

Types of Arrays

One-dimensional arrays (as shown above)
Multi-dimensional arrays (arrays within arrays)

Basic Operations on Arrays

Insert — Inserts an element at a given index
Get — Returns the element at a given index
Delete — Deletes an element at a given index
Size — Gets the total number of elements in an array

Array Processing Examples in Java

1
2
3
4
5
6
7
8
9
10
String[] dogs = {"terries", "pugs", "bulldogs", "samoyeds"};
int[] = {1, 2, 3, 4};
// Accesing an element of the array
System.out.println(dogs[1]); // Outputs pugs
// Change an element of the array
dogs[1] = "beagles";
System.out.println(dogs[1]); // Now outputs beagles
// Size of array
System.out.println(dogs.length); // Outputs 4
}

1
2
3
4
5
6
7
8
9
10
// Function to insert an element in arr at given index 
public static int[] insertElement(int[] arr, int index, int element) {
    int[] result = new int[arr.length];
    for(int i = 0; i < index; i++)
        result[i] = a[i];
    newarr[index] = element;
    for(int i = index + 1; i < arr.length; i++)
        result[i] = a[i - 1];
    return newarr;
}

Linked Lists

A linked list is another important linear data structure which might look similar to arrays at first but differs in memory allocation, internal structure and how basic operations of insertion and deletion are carried out.

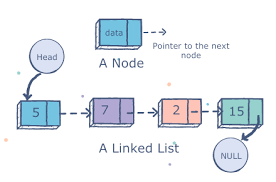A linked list is like a chain of nodes, where each node contains information like data and a pointer to the succeeding node in the chain. There’s a head pointer, which points to the first element of the linked list, and if the list is empty then it simply points to null or nothing. Linked lists are used to implement file systems, hash tables, and adjacency lists. Here’s a visual representation of the internal structure of a linked list:

Types of Linked Lists

Singly Linked List (Unidirectional)
Doubly Linked List (Bi-directional)

Basic Operations on Linked Lists

InsertAtEnd — Inserts a given element at the end of the linked list
InsertAtHead — Inserts a given element at the start/head of the linked list
Delete — Deletes a given element from the linked list
DeleteAtHead — Deletes the first element of the linked list
Search — Returns the given element from a linked list
isEmpty — Returns true if the linked list is empty

Linkled List implementation in Java

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
import java.io.*; 
public class LinkedList { 
    Node head; // head of list 
    // Linked list Node. This inner class is made static so that main() can access it 
    static class Node { 
        int data; 
        Node next; 
        Node(int d) // Constructor 
        { 
            data = d; 
            next = null; 
        } 
    } 
    // **************INSERTION************** 
    // Method to insert a new node at end
    public static LinkedList insertAtEnd(LinkedList list, int data) 
    { 
        // Create a new node with given data 
        Node new_node = new Node(data); 
        new_node.next = null; 
        // If the Linked List is empty, then make the new node as head 
        if (list.head == null) { 
            list.head = new_node; 
        } 
        else {// Else traverse till the last node and insert the new_node there 
            Node last = list.head; 
            while (last.next != null) { 
                last = last.next; 
            } 
            last.next = new_node; // Insert the new_node at last node 
        } 
        return list; 
    } 
    // **************TRAVERSAL************** 
    // Method to print the LinkedList. 
    public static void printList(LinkedList list) { 
        Node currNode = list.head; 
        System.out.print("\nLinkedList: "); 
        // Traverse through the LinkedList 
        while (currNode != null) { 
            // Print the data at current node 
            System.out.print(currNode.data + " "); 
            // Go to next node 
            currNode = currNode.next; 
        } 
        System.out.println("\n"); 
    } 
    // **************DELETION BY KEY************** 
    // Method to delete a node in the LinkedList by KEY 
    public static LinkedList deleteByKey(LinkedList list, int key) { 
        // Store head node 
        Node currNode = list.head, prev = null; 
        // CASE 1: If head node itself holds the key to be deleted 
        if (currNode != null && currNode.data == key) { 
            list.head = currNode.next; // Changed head 
            System.out.println(key + " found and deleted"); 
            // Return the updated List 
            return list; 
        } 
        // CASE 2: If the key is somewhere other than at head   
        // Search for the key to be deleted,  keep track of the previous node as it is needed to change currNode.next 
        while (currNode != null && currNode.data != key) { 
            // If currNode does not hold key continue to next node 
            prev = currNode; 
            currNode = currNode.next; 
        } 
        // If the key was present, it should be at currNode 
        // Therefore the currNode shall not be null 
        if (currNode != null) { 
            // Since the key is at currNode 
            // Unlink currNode from linked list 
            prev.next = currNode.next; 
            // Display the message 
            System.out.println(key + " found and deleted"); 
        } 
        // CASE 3: The key is not present 
        // If key was not present in linked list currNode should be null 
        if (currNode == null) { 
            System.out.println(key + " not found"); 
        } 
        return list; 
    } 
    // **************DELETION AT A POSITION************** 
    // Method to delete a node in the LinkedList by POSITION 
    public static LinkedList deleteAtPosition(LinkedList list, int index) { 
        Node currNode = list.head, prev = null; // Store head node 
        // CASE 1: If index is 0, then head node itself is to be deleted 
        if (index == 0 && currNode != null) { 
            list.head = currNode.next; // Changed head 
            System.out.println(index + " position element deleted"); 
            return list; 
        } 
        // CASE 2: If the index is greater than 0 but less than the size of LinkedList 
        int counter = 0; 
        // Count for the index to be deleted, keep track of the previous node as it is needed to change currNode.next 
        while (currNode != null) { 
            if (counter == index) { 
                // Since the currNode is the required position. Unlink currNode from linked list 
                prev.next = currNode.next; 
                System.out.println(index + " position element deleted"); 
                break; 
            } 
            else { 
                // If current position is not the index, continue to next node 
                prev = currNode; 
                currNode = currNode.next; 
                counter++; 
            } 
        }    
        // CASE 3: The index is greater than the size of the LinkedList 
        // If the position element was found, it should be at currNode, Therefore the currNode shall not be null 
        if (currNode == null) { 
            System.out.println(index + " position element not found"); 
        } 
        return list; 
    }

Bonus: Arrays vs Linked Lists

🧠 In the array the elements belong to indexes, i.e., if you want to get into the fourth element you have to write the variable name with its index or location within the square bracket. In a linked list though, you have to start from the head and work your way through until you get to the fourth element. As a result, accessing an element in an array is fast, while linked list takes linear time, so it is quite a bit slower.
🧠 Operations like insertion and deletion in array consume a lot of time. On the other hand, the performance of these operations in linked lists is fast.
🧠 Arrays are of fixed size. In contrast, linked lists are dynamic and flexible and can expand and contract its size.
🧠 In an array , memory is assigned during compile time while in a linked list it is allocated during execution or runtime.
🧠 Elements are stored consecutively in arrays whereas they are stored randomly in linked lists .

Stacks

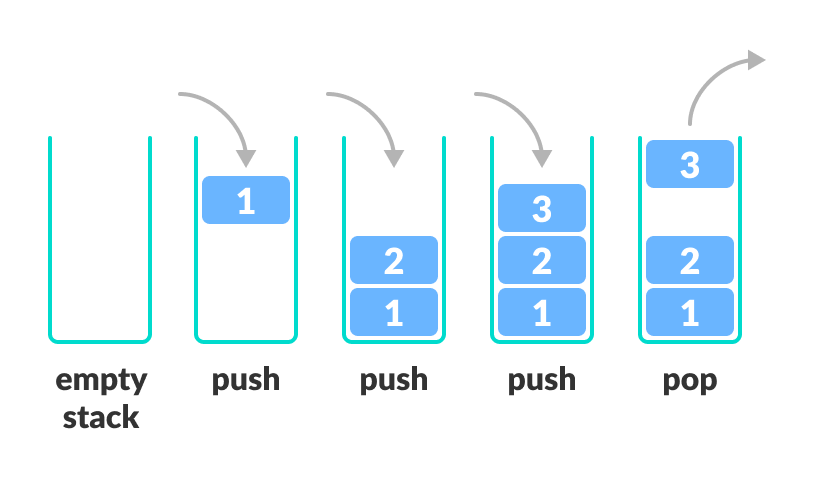We are all familiar with the Undo option, present in almost every application. Ever wondered how it works? The idea: you store the previous states of your work (which are limited to a specific number) in the memory in such an order that the last one appears first. This can’t be done just by using arrays. That is where Stacks come in. Here’s a visual representation of a stack and it's operations:

Basic Operations of Stacks

Push — Inserts an element at the top
Pop — Returns the top element after removing from the stack
isEmpty — Returns true if the stack is emptyt
Top — Returns the top element without removing from the stack

A real-life example of Stack could be a number of pancakes stacked on top of each other. In order to get the extra syrupy pancake that’s somewhere in the middle, you will need to remove (or alternatively, eat) all the pancakes placed on top of it. This is how the LIFO (Last In First Out) method works.

Stack implementation in Java

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
public class Stack<Item> implements Iterable<Item> {
    private Node<Item> first;     // top of stack
    private int n;                // size of the stack
    // helper linked list class
    private static class Node<Item> {
        private Item item;
        private Node<Item> next;
    }
    // Initializes an empty stack.
    public Stack() {
        first = null;
        n = 0;
    }
    public boolean isEmpty() {
        return first == null;
    }
    // Returns the number of items in this stack.
    public int size() {
        return n;
    }
    // Adds the item to this stack.
    public void push(Item item) {
        Node<Item> oldfirst = first;
        first = new Node<Item>();
        first.item = item;
        first.next = oldfirst;
        n++;
    }
    // Removes and returns the item most recently added to this stack.
    public Item pop() {
        if (isEmpty()) throw new NoSuchElementException("Stack underflow");
        Item item = first.item;        // save item to return
        first = first.next;            // delete first node
        n--;
        return item;                   // return the saved item
    }
    // Returns (but does not remove) the item most recently added to this stack.
    public Item top() {
        if (isEmpty()) throw new NoSuchElementException("Stack underflow");
        return first.item;
    }
     // Returns a string representation of this stack.
    public String toString() {
        StringBuilder s = new StringBuilder();
        for (Item item : this) {
            s.append(item);
            s.append(' ');
        }
        return s.toString();
    }
    // Returns an iterator to this stack that iterates through the items in LIFO order.
    public Iterator<Item> iterator() {
        return new LinkedIterator(first);
    }
    // an iterator, doesn't implement remove() since it's optional
    private class LinkedIterator implements Iterator<Item> {
        private Node<Item> current;
        public LinkedIterator(Node<Item> first) {
            current = first;
        }
        public boolean hasNext() {
            return current != null;
        }
        public void remove() {
            throw new UnsupportedOperationException();
        }
        public Item next() {
            if (!hasNext()) throw new NoSuchElementException();
            Item item = current.item;
            current = current.next; 
            return item;
        }
    }
}

Queues

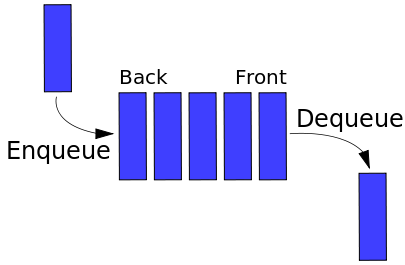Similar to Stack, Queue is another linear data structure that stores elementa in a sequential manner. The only significant difference between Stack and Queue is that instead of using the LIFO method, Queue implements the FIFO method, which is short for First in First Out.

A perfect real-life example of Queue: a line of people waiting at a ticket booth. If a new person comes, they will join the line from the end, not from the start — and the person standing at the front will be the first to get the ticket and hence leave the line.

Basic Operations of Queues

Enqueue — Inserts an element at the end of the queue
Dequeue — Removes an element from the start of the queue
isEmpty — Returns true if the queue is empty
Top — Returns the first element of the queue

Queue implementation in Java

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
public class Queue<Item> implements Iterable<Item> {
    private Node<Item> first;    // beginning of queue
    private Node<Item> last;     // end of queue
    private int n;               // number of elements on queue
    // helper linked list class
    private static class Node<Item> {
        private Item item;
        private Node<Item> next;
    }
    // Initializes an empty queue.
    public Queue() {
        first = null;
        last  = null;
        n = 0;
    }
    // Returns true if this queue is empty.
    public boolean isEmpty() {
        return first == null;
    }
    // Returns the number of items in this queue.
    public int size() {
        return n;
    }
    // Returns the item least recently added to this queue.
    public Item peek() {
        if (isEmpty()) throw new NoSuchElementException("Queue underflow");
        return first.item;
    }
    // Adds the item to this queue.
    public void enqueue(Item item) {
        Node<Item> oldlast = last;
        last = new Node<Item>();
        last.item = item;
        last.next = null;
        if (isEmpty()) first = last;
        else           oldlast.next = last;
        n++;
    }
    // Removes and returns the item on this queue that was least recently added.
    public Item dequeue() {
        if (isEmpty()) throw new NoSuchElementException("Queue underflow");
        Item item = first.item;
        first = first.next;
        n--;
        if (isEmpty()) last = null;   // to avoid loitering
        return item;
    }
    // Returns a string representation of this queue.
    public String toString() {
        StringBuilder s = new StringBuilder();
        for (Item item : this) {
            s.append(item);
            s.append(' ');
        }
        return s.toString();
    } 
    // Returns an iterator that iterates over the items in this queue in FIFO order.
    public Iterator<Item> iterator()  {
        return new LinkedIterator(first);  
    }
    // an iterator, doesn't implement remove() 
    private class LinkedIterator implements Iterator<Item> {
        private Node<Item> current;
        public LinkedIterator(Node<Item> first) {
            current = first;
        }
        public boolean hasNext() { 
		return current != null;                     
	}
        public void remove() { 
		throw new UnsupportedOperationException();  
	}
        public Item next() {
            if (!hasNext()) throw new NoSuchElementException();
            Item item = current.item;
            current = current.next; 
            return item;
        }
    }
}

Binary Search Trees

Tree walks in Java

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
// java program for different tree traversals
class Node {
    int key;
    Node left, right;

    public Node(int item)    {
        key = item;
        left = right = null;
    }
}

class BinaryTreeWalk {
    // root of Binary Tree
    Node root;

    BinaryTreeWalk() {
        root = null;
    }

    // given a binary tree, print its nodes according to the "bottom-up" postorder traversal. */
    void printPostorder(Node node) {
        if (node == null)
            return;

        // first recur on left subtree
        printPostorder(node.left);

        // then recur on right subtree
        printPostorder(node.right);

        // now deal with the node
        System.out.print(node.key + " ");
    }

    // given a binary tree, print its nodes in inorder
    void printInorder(Node node) {
        if (node == null)
            return;

        // first recur on left child
        printInorder(node.left);

        // then print the data of node
        System.out.print(node.key + " ");

        // now recur on right child
        printInorder(node.right);
    }

    // given a binary tree, print its nodes in preorder
    void printPreorder(Node node) {
        if (node == null)
            return;

        // first print data of node
        System.out.print(node.key + " ");

        // then recur on left sutree
        printPreorder(node.left);

        // now recur on right subtree
        printPreorder(node.right);
    }

    // Wrappers over above recursive functions
    void printPostorder() {
        printPostorder(root);
    }

    void printInorder() {
        printInorder(root);
    }

    void printPreorder() {
        printPreorder(root);
    }

    public static void main(String[] args) {
        BinaryTreeWalk tree = new BinaryTreeWalk();
        tree.root = new Node(1);
        tree.root.left = new Node(2);
        tree.root.right = new Node(3);
        tree.root.left.left = new Node(4);
        tree.root.left.right = new Node(5);

        System.out.println("Preorder traversal of binary tree is ");
        tree.printPreorder();

        System.out.println("\nInorder traversal of binary tree is ");
        tree.printInorder();

        System.out.println("\nPostorder traversal of binary tree is ");
        tree.printPostorder();
    }
}

Hash Tables

Collisions resolved by chaining in Java

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
// Java program to demonstrate implementation of our own hash table with chaining for collision detection
import java.util.ArrayList;

// A node of chains
class HashNode<K, V> {
    K key;
    V value;

    // Reference to next node
    HashNode<K, V> next;

    // Constructor
    public HashNode(K key, V value) {
        this.key = key;
        this.value = value;
    }
}

// Class to represent entire hash table
class ChainingHash<K, V> {
    // bucketArray is used to store array of chains
    private ArrayList<HashNode<K, V>> bucketArray;

    // Current capacity of array list
    private int numBuckets;

    // Current size of array list
    private int size;

    // Constructor (Initializes capacity, size and empty chains.
    public ChainingHash() {
        bucketArray = new ArrayList<>();
        numBuckets = 10;
        size = 0;

        // Create empty chains
        for (int i = 0; i < numBuckets; i++)
            bucketArray.add(null);
    }

    public int size() {
        return size;
    }

    public boolean isEmpty() {
        return size() == 0;
    }

    // This implements hash function to find index for a key
    private int getBucketIndex(K key) {
        int hashCode = key.hashCode();
        int index = hashCode % numBuckets;
        return index;
    }

    // Method to remove a given key
    public V remove(K key) {
        // Apply hash function to find index for given key
        int bucketIndex = getBucketIndex(key);

        // Get head of chain
        HashNode<K, V> head = bucketArray.get(bucketIndex);

        // Search for key in its chain
        HashNode<K, V> prev = null;
        while (head != null) {
            // If Key found
            if (head.key.equals(key))
                break;

            // Else keep moving in chain
            prev = head;
            head = head.next;
        }

        // If key was not there
        if (head == null)
            return null;

        // Reduce size
        size--;

        // Remove key
        if (prev != null)
            prev.next = head.next;
        else
            bucketArray.set(bucketIndex, head.next);

        return head.value;
    }

    // Returns value for a key
    public V get(K key) {
        // Find head of chain for given key
        int bucketIndex = getBucketIndex(key);
        HashNode<K, V> head = bucketArray.get(bucketIndex);

        // Search key in chain
        while (head != null) {
            if (head.key.equals(key))
                return head.value;
            head = head.next;
        }

        // If key not found
        return null;
    }

    // Adds a key value pair to hash
    public void add(K key, V value) {
        // Find head of chain for given key
        int bucketIndex = getBucketIndex(key);
        HashNode<K, V> head = bucketArray.get(bucketIndex);

        // Check if key is already present
        while (head != null) {
            if (head.key.equals(key))
            {
                head.value = value;
                return;
            }
            head = head.next;
        }

        // Insert key in chain
        size++;
        head = bucketArray.get(bucketIndex);
        HashNode<K, V> newNode = new HashNode<K, V>(key, value);
        newNode.next = head;
        bucketArray.set(bucketIndex, newNode);

        // If load factor goes beyond threshold, then double hash table size
        if ((1.0*size)/numBuckets >= 0.7) {
            ArrayList<HashNode<K, V>> temp = bucketArray;
            bucketArray = new ArrayList<>();
            numBuckets = 2 * numBuckets;
            size = 0;
            for (int i = 0; i < numBuckets; i++)
                bucketArray.add(null);

            for (HashNode<K, V> headNode : temp) {
                while (headNode != null) {
                    add(headNode.key, headNode.value);
                    headNode = headNode.next;
                }
            }
        }
    }

    // Driver method to test Map class
    public static void main(String[] args) {
        ChainingHash<String, Integer>map = new ChainingHash<>();
        map.add("this",1 );
        map.add("coder",2 );
        map.add("this",4 );
        map.add("hi",5 );
        System.out.println(map.size());
        System.out.println(map.remove("this"));
        System.out.println(map.remove("this"));
        System.out.println(map.size());
        System.out.println(map.isEmpty());
    }
}

Open-addressing implementation in Java

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
 public class OpenAddressingHash {
    // properties of hash table
    private int max = 20;
    private HashTableNode[] vector = new HashTableNode[max];

    // element of hash table.
    class HashTableNode {
        public int key;

        HashTableNode(int key) {
            this.key = key;
        }
    }

    // constructor
    OpenAddressingHash() {
        for (int i = 0; i < max; i++) {
            this.vector[i] = null;
        }
    }

    // add element to hash table
    public void insert(int key, int i) {
        int hashcode = this.hashFunction(key, i);

        if ((i > 0) && (hashcode == this.hashFunction(key, 0))) {
            System.out.println("It's not possible to add the key " + key + " in hash table.");
            return;
        }

        if (this.vector[hashcode] != null) {
            this.insert(key, i + 1);
        }

        else {
            this.vector[hashcode] = new HashTableNode(key);
        }
    }

    // overloading of add() method. Simplifies the call of method.
    public void insert(int key) {
        this.insert(key, 0);
    }

    // search an element in hash table.
    public int search(int key, int i) {
        int hashcode = this.hashFunction(key, i);

        if ((i > 0) && (hashcode == this.hashFunction(key, 0))) {
            System.out.println("Key " + key + " not found in hash table. It was made " + i + " stepsizes.");
            return -99;
        }

        if ((this.vector[hashcode] != null) && (this.vector[hashcode].key == key)) {
            System.out.println("Key " + key + " found in hash table in " + (i + 1) + "-esim stepsize.");
            return hashcode;
        }

        return this.search(key, i + 1);
    }

    // overloading of search() method. Simplifies the call of method.
    public int search(int key) {
        return this.search(key, 0);
    }

    //Remove an element from the hash table.
    public void delete(int key) {

        int i = this.search(key);

        if (i != -99) {
            System.out.println("The key " + key + " was removed from hash table.");
            this.vector[i] = null;
        }
        else {
            System.out.println("The key " + key + " was not removed, because it does not exists in hash table.");
        }
    }

    // linear probing
    public int linearProbing(int key, int i) {
        return (key + i) % this.max;
    }

    // quadratic probing.
    public int quadraticProbing(int key, int i) {
        return (key + (i * i)) % this.max;
    }

    // double hashing.
    public int doubleHash(int key, int i) {
        return (this.doubleHash2(key) + i) % this.max;
    }

    // auxiliar hash function to Double hashing made by double() method.
    public int doubleHash2(int key) {
        return (1 + key) % (this.max - 1);
    }

    // hash function.
    public int hashFunction(int key, int i) {
        return this.linearProbing(key, i);
    }

    // toString method.
    public String toString() {
        String description = "Hash table: [ ";
        for (int i = 0; i < this.max; i++) {
            if (this.vector[i] == null) {
                description += "__  ";
            }
            else {
                description += String.format("%2d  ", this.vector[i].key);
            }
        }
        description += "]";
        return description;
    }
}